9 Variablen, Funktionen und Operatoren
Dieses Kapitel vertieft die Basistechniken zur Adressierung. Es zeigt, wie Konstanten und Variablen in Excel erstellt werden und wie Funktionen und Operatoren in Excel-Formeln zur Lösung komplexer Probleme eingesetzt werden. Neben Operatoren und Funktionen formalisiert dieses Kapitel die beiden Excel-Dekoratoren = und '.
Es werden die folgenden Operatoren und Funktionen behandelt: :, .:, :., .:., #, @, +, -, *, /, %, ^, &, =, >, <, <=, >=, <>, TEXTKETTE(), (Leerschlagoperator), SEQUENZ(), ZUFALLSMATRIX(), LET(), LAMBDA(), MAP(), REDUCE(), NACHZEILE(), NACHSPALTE(), SCAN()
9.1 Variablen
Excel kennt keine strikte Unterscheidung zwischen Konstanten und Variablen. Grundsätzlich sind alle Werte in Excel Konstanten, weil direkt eingegebene oder durch eine Formel erzeugte Werte nicht durch andere Formel verändert werden können.
In Excel lassen sich Zellen und Bereiche sperren. Damit lassen sich die Werte wie Konstanten behandeln. Diese Sperre ist Teil der Formatierung einer Zelle und muss für das gesamte Arbeitsblatt festgelegt werden. Die Sperre kann nicht für einzelne Zellen oder Bereiche festgelegt werden.
Die Sperre eines Arbeitsblatts wird im Menuband Überprüfen mit dem Kommando Blatt schützen aktiviert. Richten Sie bei diesem Kommando kein Passwort ein.
Ist ein Arbeitsblatt gesperrt, sind die Werte auf diesem Arbeitsblatt unveränderlich und verhalten sich wie Konstanten. Ist ein Arbeitsblatt nicht gesperrt, dann verhalten sich die Werte wie Variablen.
Bezeichner unterliegen in Excel Beschränkungen. Es dürfen also nicht beliebige Bezeichner verwendet werden, sondern nur jene, die folgende Regeln einhalten.
- Bezeichner dürfen nur aus Buchstaben, Zahlen, Dollarzeichen, Punkten und Unterstrichen (
_) bestehen. - Bezeichner dürfen keine bestehenden Funktionsnamen sein.
- Bezeichner dürfen keine gültigen Adressen im A1-Format sein.
- Bezeichner dürfen keine gültigen Adressen im Z1S1-Format sein.
Beispiel 9.1 (Ungültiger Bezeichner) Der Bezeichner x1 ist ungültig, weil dieser identisch mit der Adresse X1 wäre. Wird Bezeichner um einen Unterstrich zu x_1 erweitert, dann gibt es keine Kollision mit der Adresse mehr und der Bezeichner ist gültig.
9.1.1 Benannte Bereiche
Im Funktionsbalken wird ganz links die Adresse der aktuellen Zelle angezeigt. Wenn in dieses Feld geklickt wird, dann kann der Adresse ein Name zugewiesen werden. Auf diese Weise kann eine Zelle oder ein Bereich benannt werden. Der Name eines Bereichs darf nur einmal in einer Arbeitsmappe existieren. Dafür kann in jeder Zelle der Arbeitsmappe dieser Namen als Adresse verwendet werden. Dazu ist es nicht notwendig, den die genaue Arbeitsblatt- und Zelladresse zu kennen.
Verweist ein benannter Bereich mit einer Zelle auf den Anfang eines dynamischen Bereichs, dann kann der gesamte dynamische Bereich mit der Gatter-Notation referenziert werden.
Auf diese Weise lassen sich oft adressierte Zellen oder Bereiche benennen. Dadurch kann die Adresse für Verwendung in Formeln abstrahiert werden.
Die Verwendung von benannten Bereichen wird weiter vereinfacht, dass bei der Eingabe von Formeln die Namen der benannten Bereiche als Vorschlag angezeigt werden.
Beispiel 9.2 (Adressierung eines dynamischen benannten Bereichs)
=umsatz#Benannte Zellen helfen, auf wichtige Zellen in einer Arbeitsmappe zuzugreifen.
Ein benannter Bereich entspricht einer Variablen in anderen Programmiersprachen.
Eine benannte Zelle oder ein benannter Bereich sind immer absolut referenziert.
Wenn einem benannten Bereich Zellen hinzugefügt werden, dann wird der benannte Bereich um diese Zellen erweitert.
Eine Tabelle ist ein spezieller benannter Bereich, der als Ganzes oder in Teilen referenziert werden kann (s. Abschnitt 5.2.4).
9.2 Arbeitsmappennamen
Benanntebereiche eignen sich besonders für variable Werte, welche durch Anwender geändert werden können und dürfen. Konstante Werte sind Werte, die nicht interaktiv geändert werden dürfen. Um solche Konstanten zu spezifizieren, wird Excels Namens-Manager (s. Abbildung 9.1) verwendet.

Formeln
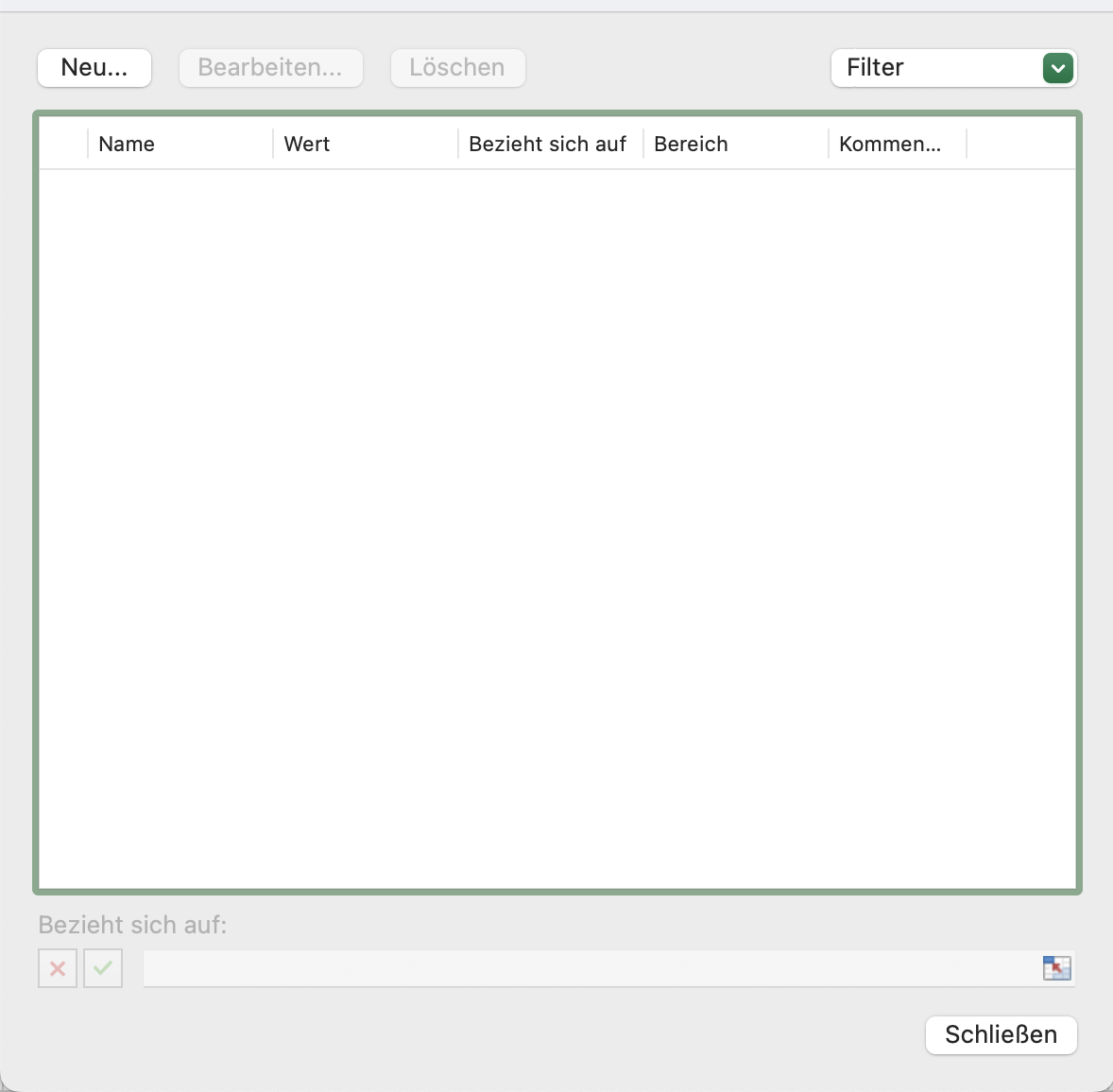
So definierte Namen stehen in der gesamten Arbeitsmappe zur Verfügung.
9.3 Operatoren
Operatoren sind spezielle Symbole in Formeln, die zur Verknüpfung von Werten dienen.
Excel unterscheidet zwischen den folgenden Operatoren:
- Adressoperatoren (Bezugsoperatoren, s. Kapitel 5.2)
- Arithmetische Operatoren
- Vergleichsoperatoren
- Textoperatoren
9.3.1 Adressoperatoren
Mit Adressoperatoren lassen sich Adressen zu Bereichen verknüpfen. Diese Bereiche werden in der Regel als Vektoren oder Matrizen (s. Kapitel 12) behandelt.
Excel stellt sieben Adressoperatoren bereit:
Die vier Doppenpunktoperatoren:
:.:.:.:.
Den Feld- bzw. dynamischen Feldoperator:
#
Der linke Operand steht bei allen diesen Operatoren für die linke obere Zelle. Diese Zelle heisst Startzelle des Bereichs. Für die ersten vier Operatoren steht der rechte Operand für die rechte untere Zelle, welche als Endzelle des Bereichs bezeichnet wird.
Wird bei den Doppelpunktoperatoren die Start- und Endzelle vertauscht, passt Excel die Adressierung so an, damit die Bereichsadresse der oben genannten Konvention entspricht.
Beispiel 9.3 (Verdrehte Bereichsadressierungen für den Bereich B3:D7)
B7:D3
D7:B3
D3:B79.3.1.1 Schnittstellenoperator
Eine Besonderheit ist der Schnittmengenoperator oder auch Leerschlagopertor (). Dieser Operator liefert aus zwei sich überschneidenden Bereichen die sich überschneidenden Werte. Falls sich die angegebenen Bereiche nicht überschneiden, wird der #NULL!-Fehler erzeugt.
Beispiel 9.4 (Der Schnittmengenoperator)
H10:M16 K13:O19Diese Adresse gibt den Bereich K13:M16 zurück.
9.3.1.2 Der Gleiche-Zeile-Operator
Der “Gleiche-Zeile”-Operator bzw. der “implizite Schnittmengen”-Operator (@) zeigt an, dass Werte an der gleichen Position verwendet werden sollen. Dieser Prefix-Operator unterscheidet sich im Verhalten je nachdem ob er auf Adress- oder Tabellenbereiche angewandt wird.
Diese besondere Stärke der @-Addressierung kommt in Tabellenformeln zum Tragen. Tabellenformeln sind Formeln, die Berechnungen in einer eigenen Tabellespalte durchführen. Wird in solchen Formeln eine Tabellenadresse in der gleichen Tabelle mit @ eingeleitet, dann bedeutet der Operator, dass der Wert in der gleichen Zeile verwendet werden soll und nicht die gesamte Spalte (s. Beispiel 9.5).
Beispiel 9.5 (@-Operator in einer Tabellenformel) Addiere auf den Wert in Spalte foo 1 hinzu.
=[@foo] + 1Wird der @-Operator für eine Adresse in einer anderen Tabelle verwendet, dann müssen die Wertebereiche beider Tabellen in der gleichen Zeile starten, weil der @-Operator erfordert, dass die referenzierte Adresse in der gleichen Arbeitsblattzeile und nicht in der gleichen Tabellenzeile steht. Verweist eine @-Adressierung auf eine Tabellenspalte, die an der gleichen Arbeitsblattzeile keinen Wert hat, dann erzeugt der Operator einen #WERT!-Fehler (s. Abbildung 9.2).
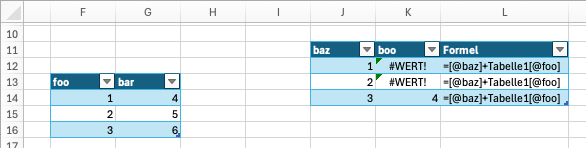
@
Wird der @-Operator für Arbeitsblattbereiche verwendet, dann muss die entsprechende Formel an der gleichen Arbeitsblattzeile und Arbeitsblattspalte stehen. Das ist nur möglich, wenn die Formel auf einem anderen Arbeitsblatt steht. Diese Beschränkung zeigt an, dass dieser Operator nicht für die Referenzierung von Arbeitsblattbereichen verwendet werden sollte.
Beispiel 9.6 (Arbeitsblattadresse mit @-Operator)
= @Tabelle1!AB10#Diese Formel muss an einer gültigen Adresse ab AB10 auf einem anderen Arbeitsblatt stehen.
9.3.2 Arithmetische Operatoren
Excel stellt sechs Arithmetische Operatoren zur Verfügung.
| Operator | Bedeutung |
|---|---|
+ |
Addition |
- |
Subtraktion oder negatives Vorzeichen (Multiplikation mit -1) |
* |
Multiplikation |
/ |
Division |
% |
Prozent (Division durch 100) |
^ |
Potenz (z.B. 2 ^ 3 entspricht 2^3) |
9.3.3 Vergleichsoperatoren
Excel verwendet die bekannten sechs Vergleichsoperatoren. Die Vergleichsoperatoren werden in Kapitel 11 im Abschnitt Vergleiche behandelt.
=><>=<=<>(ungleich)
9.3.4 Textoperator
Excels Text- bzw. Textkettenoperator & verknüpft zwei Zeichenketten. Dieser Operator ist gleichwertig mit der Funktion TEXTKETTE() mit genau zwei Parametern. unabhängig vom Datentyp der Operandenden ist das Ergebnis dieser Operation immer eine Zeichenkette.
Beispiel 9.7 (Verwendung des &-Operators) Fügt ein Ausrufezeichen zum Wert in Adresse A1
= A1 & "!"9.4 Dekoratoren
Definition 9.1 Ein Dekorator ist Sprachelement einer Programmiersprache, mit dem die normale Interpretation von Symbolen verändert werden kann.
Excel hat zwei Dekoratoren. Diese Dekoratoren müssen immer als erstes Symbol einer Zelle stehen. D.h. es dürfen auch keine Leerzeichen vor einem Dekorator stehen. Die beiden Dekoratoren sind:
- Der Apostroph-Dekorator (
') - Der Gleich-Dekorator (
=)
9.4.1 Apostroph-Dekoraktor
Der Apostroph-Dekorator (') erzwingt, dass die nachfolgenden Symbole als Zeichenkette interpretiert werden müssen.
Mithilfe des Apostroph-Dekorators wird die automatische Typerkennung für die laufende Eingabe deaktiviert. Auf diese Weise lassen sich Zeichenketten eingeben, die nur aus Ziffern bestehen oder Zeichenketten, die Datentumswerten ähneln.
Der Apostroph-Dekorator muss zwingend verwendet werden, wenn auf eine Zeichenkette eine der folgenden Bedingungen zutrifft.
- Die Zeichenkette beginnt mit einem Gleichheitszeichen (
=), einem Pluszeichen (+), einem Minuszeichen (-) oder einem Prozentzeichen (%). - Die Zeichenkette besteht nur aus Ziffern, dem Dezimaltrenner (
.) oder dem Tausendertrenner (‘) enthält - Die Zeichenkette ähnelt der wissenschaftliche Notation für Zahlen mit und ohne Vorzeichen für den Exponenten. Z.B.
5.E3. - Die Zeichenkette ähnelt einem Datum.
- Die Zeichenkette entspricht einen Fehlerwert, unabhängig von der Schreibweise. Z.B.
#nv. - Die Zeichenkette entspricht einem Wahrheitswert (
WAHRoderFALSCH) unabhängig von der Schreibweise.
Das Apostroph kann entfallen, wenn die aktive Zelle vorher bereits als Datentyp Text formatiert wurde. In diesem Fall verlieren alle Symbole ihre spezielle Bedeutung. In solche Zellen können keine Formeln eingegeben werden.
9.4.2 Gleich-Dekorator
Der Gleich-Dekorator (=) zeigt an, dass die nachfolgenden Symbole als Formel interpretiert werden müssen.
Bei der Eingabe des Gleich-Dekorators wechselt Excel für die laufende Eingabe in den Formelmodus. Mit beenden der Eingabe mit der Eingabetaste wird der Formelmodus wieder verlassen und das Ergebnis der eingegebenen Formel wird in der Zelle angezeigt.
9.5 Funktionen
Excel kann nur durch Funktionen und Operatoren programmiert werden.
Excel hat wenige vordefinierte Operatoren, wobei die Operatoren keine direkte Entsprechung als Funktion haben. Die einzige Ausnahmen sind der Potenzoperator (^) und der Textverkettungsoperator (&). Der Potenzoperator ist funktional gleich mit der POTENZ()-Funktion. Der Textverkettungsoperator entspricht der Funktion TEXTKETTE() mit zwei Argumenten.
Die mit Excel möglichen Programme sind durch die Operatoren und die vordefinierten Funktionen beschränkt.
Excel Kommandos können nur durch Interaktion mit den Excel Menus oder Dialogen ausgeführt werden. Diese Funktionalität steht für die Progammierung oft nicht zur Verfügung.
Neben den Funktionen und Kommandos existieren in Excel noch Makros. Mit Makros können neue Kommandos und Funktionen programmiert werden. Makros folgen aber nicht den Regeln von Formeln, weil sie in einer anderen Programmiersprache geschrieben werden.
Makros unterliegen nicht den Einschränkungen von Excel-Funktionen. Diese Freiheit ist gleichzeitig ein Fluch, denn Makros sind ein Sicherheitsrisiko und Excel präsentiert entsprechende Warnungen, wenn Makros in einer Arbeitsmappe gefunden wurde.
Aktuelle Bestrebungen von Microsoft zielen darauf ab, Makros langfristig durch Funktionen zu ersetzen. Ein Teil dieser Bestrebungen ist die Einführung von LAMBDA()-Funktionen (s. Abschnitt 9.8).
Excel hat keine Identitätsfunktion. Die Identitätsfunktion wird durch eine Formel simuliert, die nur eine Adresse enthält. Solche Formeln werden für das Vektorisieren (Definition 5.6) von Bereichen eingesetzt.
9.5.1 Generatoren in Excel
Excel hat zwei Generatorfunktionen:
- Die
SEQUENZ()-Funktion - Die
ZUFALLSMATRIX()-Funktion
Beide Generatoren erfordern die Anzahl der Zeilen und Spalten, für die Werte generiert werden sollen. Soll nur ein Spaltenvektor erzeugt werden, muss nur die Anzahl der Zeilen angegeben werden.
Die SEQUENZ()-Funktion erzeugt eine Sequenz von Werten ausgehend vom ersten Wert (Anfang). Die Schrittweite legt die Abstände zwischen den einzelnen Werten fest. Standardmässig ist die Schrittweite mit 1 festgelegt.
Wird die Schrittweite mit 0 festgelegt, dann wird der Anfangswert für die angegebene Anzahl von Spalten und Zeilen wiederholt.
Die Funktion ZUFALLSMATRIX() erzeugt Zufallswerte in einem vorgegebenen Intervall. Diese Funktion kann reelle Zahlen oder ganze Zahlen generieren. Der Wertebereich der generierten Zahlen kann durch einen Minimal- und einem Maximalwert eingeschränkt werden. Wird kein Minimal- und Maximalwert angegeben, dann werden Werte im Intervall 0 < z < 1 generiert. Werden Ganzzahlen für dieses Intervall angefordert, dann werden die Werte 0 und 1 erzeugt.
9.6 Substitution
Excel kennt zwei Formen der Substitution.
- Die Substitution über Funktionspfade
- Die Substitution mit der Funktion
LET()
Beide Substitutionsformen sind fast gleichwertig. Funktionspfade eigenen sich besonders gut für die Entwicklung von und zur Fehlersuche in komplexen Formeln. LET() erlaubt es, mehrere Arbeitsschritte effizient in einer Formel zusammenzufassen.
9.6.1 Substitution über Funktionspfade
Eine komplexe Operation lassen sich in Excel durch Substitution über Funktionspfade vereinfachen.
Definition 9.2 Ein Funktionspfad sind Formeln, die sich über ihre Adressen aufeinander beziehen.
Bei einem Funktionspfad werden die substituierten Funktionen als Formeln in separate Zellen geschrieben. Die Adresse der jeweiligen Formel wird als Substitution für die Funktion eingesetzt. Sind die Formeln in einem benannten Bereich, dann kann der Name des Bereichs zur Substitution verwendet werden.
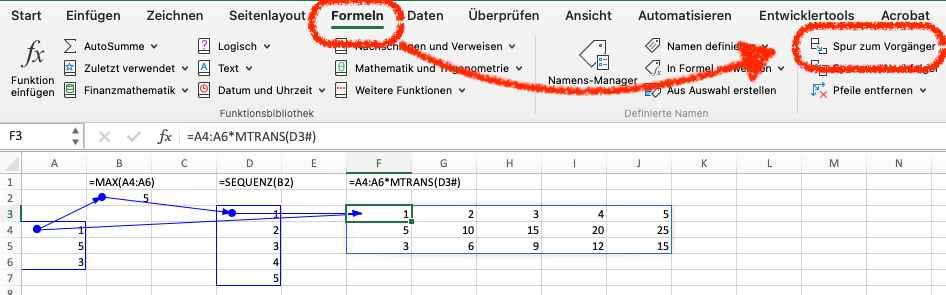
Funktionspfade können mithilfe des Kommandos Spur zum Vorgänger im Menü Formeln sichtbar gemacht werden (Abbildung 9.3).
Um komplexe Formeln in bestehenden Arbeitsmappen zu verstehen, hilft das Zerlegen dieser Formeln in Funktionspfade. Dabei kann eine tabellarische Organisation helfen, wiederkehrende Operationen leichter zu erkennen.
9.6.2 Substitution mit LET()
Excels LET()-Funktion erlaubt das Vereinfachen komplizierter Formeln durch Variablen. Diese Variablen existieren nur im Kontext der LET()-Funktion und können nicht ausserhalb dieser Funktion verwendet werden.
Eine Variable in der LET()-Funktion entspricht einer Substitution eines Teilausdrucks einer Formel.
Beispiel 9.8 (LET()-Funktion zur Substitution)
=LET(
Daten; 'Unbearbeitete Daten'!A:F;
DatenFeld; INDEX(
Daten;
sequenz(ZEILEN(Daten));
sequenz(1; SPALTEN(Daten))
);
WENN(ISTLEER(DatenFeld);#NV;DatenFeld)
)In Beispiel 9.8 wird der referenzierte Bereich und der Aufruf der INDEX() substituiert. Die Substitution wird durch die Variablen Daten und DatenFeld realisiert.
Beispiel 9.9 (Formel ohne Substitution)
=WENN(ISTLEER(INDEX(
'Unbearbeitete Daten'!A:F;
sequenz(ZEILEN('Unbearbeitete Daten'!A:F));
sequenz(1; SPALTEN('Unbearbeitete Daten'!A:F))
));
#NV;
INDEX(
'Unbearbeitete Daten'!A:F;
sequenz(ZEILEN('Unbearbeitete Daten'!A:F));
sequenz(1; SPALTEN('Unbearbeitete Daten'!A:F))
)
)Die beiden Beispiele veranschaulichen, wie mit der LET()-Funktion mehr als eine Substitution umgesetzt wird, um eine komplexe Formel in überschaubare Teilschritte zu zerlegen und so stark zu vereinfachen.
Wird eine Funktion in einer Formel mit den gleichen Parametern mehrfach aufgerufen, dann sollte diese Funktion immer mit LET() substituiert werden. Substituierte Berechnungen werden nur einmal für die Substitution durchgeführt und anschliessend wird nur das Ergebnis verwendet. Nicht substituierte Funktionen werden bei jedem Vorkommen neu ausgeführt.
9.7 Funktionsketten
Funktionsketten werden in Excel über Substitutionen erzeugt. Gerade bei Matrizen und anderer Transformationen von Datenstrukturen ist die Verwendung von Funktionspfaden aus zwei Gründen unhandlich:
- Wenn die Ergebnisse mehrerer Arbeistsschritte auf einem Arbeitsblatt dargestellt werden, wird die Übersichtlichkeit behindert.
- Weil Funktionspfade separate Formeln verwenden werden die Ergebnisse für jede Formel serialisiert, was nicht immer zu den erwarteten Ergebnissen führt.
Weil Excel keine Operatoren für die Funktionsverkettung bereitstellt, werden Funktionsketten immer mithilfe der Funktion LET() erzeugt.
9.7.1 LET() und leere Zellen
Normalerweise werden leere Zellen als Ergebnis einer Funktion durch 0 ersetzt. Dieses Konvertierung findet erst bei der Darstellung des Ergebnisses statt. Innerhalb einer Funktionskette werden leere Zellen als leere Zellen weitergereicht, solange keine Aggregation vorgenommen wird. Es ist deshalb möglich in einer Funktionskette eine Entscheidung mit ISTLEER() für den Fall einer leeren Zelle zu treffen.
Eine Excel-Operation muss einen Wert als Ergebnis einer Formel haben. Wird ein nicht vorhandener Wert (d.h. leere Zelle) in einem Ergebnis einer Formel gefunden, dann wird dieser Wert automatisch in den Wert 0 konvertiert. Diese Umwandlung passiert jedoch erst nachdem die Operation abgeschlossen ist und Excel das Ergebnis auf dem Arbeitsblatt darstellt.
Dieses Verhalten hat zur Folge, dass solange eine Operation nicht abgeschlossen ist, die nicht vorhandenen Werte in ihrer ursprünglichen Form erhalten bleiben. Es ist also möglich undefinierte Werte mit ISTLEER() zu prüfen.
Die ursprünglichen Daten können unvollständig sein und enthalten dann leere Zellen an den entsprechenden Zellen. Diese fehlenden Werte als 0 darzustellen, kann zu verzerrten Ergebnissen führen. Deshalb sollten solche Werte mit dem Fehler #NV (lies: Nicht Vorhanden) markiert werden. Dieser Fehlerwert wird nicht automatisch in den Wert 0 umgewandelt, so dass die fehlenden Werte korrekt berücksichtigt werden können.
Diese Umwandlung nutzt aus, dass Excel leere Zellen als Ergebnis von Funktionen zulässt, aber nicht als Ergebnis von Formeln. Entsprechend kann das folgende Funktionsmuster verwendet werden.
Die beiden Vektoren G1# und H1# sind Hilfsvektoren, die Sequenzen für die Zeilen- und Spaltenindizes der Datenstruktur A:F enthalten.
Der logische Ausdruck prüft, ob ein Feld mit dem Index G1# und H1# im Stichprobenobjekt leer ist. Falls das Feld in den unbearbeiteten Daten leer ist, dann wird der Wert #NV als Ergebnis zurückgegeben. Sonst soll der Wert im Feld übergeben.
In dieser Operation wird die Funktion INDEX() zwei Mal mit den gleichen Parametern aufgerufen. Das ist unpraktisch, weil die Operation an zwei Stellen angepasst müsste, wenn die Daten mehr oder weniger Spalten haben. Besser wäre es, wenn das Zwischenergebnis der INDEX()-Funktion aus der Operation herausgelöst wird und über eine Funktionsverkettung eingebunden wird. Das ist aber nicht möglich, weil Excel bei diesem Zwischenschritt die fehlenden Werte in 0 ändert, sodass anschliessend der logische Ausdruck immer FALSCH liefern würde.
Mittels der LET() Funktion wird das Ergebnis dieses Zwischenschritts in einer temporären Variablen gespeichert. Gegenüber der normalen Funktionsverkettung durch Funktionspfade hat diese Strategie den Vorteil, dass für Excel die Operation nicht abgeschlossen ist und deshalb die fehlenden Werte noch nicht in den Wert 0 umgewandelt werden. Der logische Ausdruck in der WENN()-Funktion kann also WAHR ergeben, wenn in den Daten ein Wert fehlt. Ausserdem muss die Indizierung für eine Position nur einmal durchgeführt werden, was bei komplexen Formeln die Übersichtlichkeit erhöht und die Ausführung beschleunigt.
Die Namen in der LET() unterliegen den gleichen Beschränkungen, wie alle anderen Bezeichner (Abschnitt Kapitel 9.1).
Die ursprüngliche Formel lässt sich also dahingehend vereinfachen, dass der Aufruf der INDEX()-Funktion “ausgeklammert” und in der Hilfsvariablen Feld gespeichert wird.
Daraus ergibt sich die Lösung als Funktionskette.
=LET(Feld; INDEX('Unbearbeitete Daten'!A:F;A2#;B1#);
WENN(
ISTLEER(Feld);
#NV;
Feld
)
)Diese Lösung entspricht ungefähr der Funktionskette Formel 9.1.
Index() \triangleright Wenn() \tag{9.1}
Damit wird der Aufruf der WENN()-Funktion vereinfacht, weil nur noch die Hilfsvariable Feld übergeben müssen. Diese Variable enthält die Daten für die Funktionsverkettung, so dass eine zusätzliche Arbeitsblattadresse nicht notwendig ist.
9.8 Funktionen selbst definieren
In Excel können eigene Funktionen mit der Funktion LAMBDA() erzeugt werden. Die LAMBDA()-Funktion erzeugt die Funktion aus ihren Parametern. Dabei ist der letzte Parameter immer der Funktionskörper. Die restlichen Parameter sind die Parameter der Funktion. Es können max 253 Parameter angegeben werden, wobei keine optionalen oder vorbelegten Parameter möglich sind. Beispiel 9.10 zeigt eine einfache Funktionsdefinition mit zwei Parametern.
Beispiel 9.10 (Funktionsdefinition mit zwei Parametern ohne Ausführung)
= LAMBDA(a; b; a + b)Mit Excels LAMBDA()-Funktion können nur Funktionen durch Verkettung anderer Funktionen erzeugt werden.
Für Excel sind Funktionen kein darstellbarer Datentyp. Wird also eine Funktion mit LAMBDA() definiert, ohne dass sie unmittelbar ausgeführt wird, zeigt Excel den Fehler #KALK! an. Dieser Fehler kann dadurch vermieden werden, indem die Funktion unmittelbar ausgeführt wird (s. Beispiel 9.11).
Beispiel 9.11 (Funktionsdefinition mit zwei Parametern mit sofortiger Ausführung)
= LAMBDA(a; b; a + b)(1;2)Der Funktionskörper muss nicht alle Parameter verwenden. Wird eine Funktion aufgerufen, dann müssen alle Parameter angegeben werden, selbst wenn diese im Funktionskörper nicht verwendet werden.
9.8.1 Map-Reduce und LAMBDA()
Weil eine mit LAMBDA() erzeugte Funktion als Formel direkt ausgeführt werden muss, ergibt sich kein Vorteil gegenüber normalen Excel-Formeln. Die Funktion wird jedoch zum Erstellen von Callbacks benötigt. Die Hauptanwendung sind Operationen, die mit jedem Wert eines Bereichs durchgeführt werden sollen. Weil Excel normalerweise keine Schleifen zulässt, müssen solche Operationen über die Logikfunktionen MAP(), NACHZEILE(), NACHSPALTE(), REDUCE() und SCAN() erzeugt werden.
Alle Map-Funktionen erwarten als ersten Parameter einen Bereich mit Werten und als letzten Parameter eine Funktionsdefinition mit LAMBDA().
MAP()erzeugt eine Schleife, welche den Callback für jedes Element genau einmal aufruft. Es ist möglich, mehrere Bereiche anzugeben. Die Parameteranzahl der Callback muss der Anzahl der angegebenen Bereiche entsprechen.NACHSPALTE()erzeugt eine Schleife, die eine Funktion für jede Spalte eines Bereichs aufruft. Der Callback darf nur einen Parameter haben. Der Parameter enthält eine Liste mit allen Werten der aktuellen Zeile.NACHZEILE()erzeugt eine Schleife, die eine Funktion für jede Zeile eines Bereichs aufruft. Der Callback darf nur einen Parameter haben.
MAP(), NACHSPALTE() und NACHZEILE() behandeln die einzelnen Durchläufe der Schleife als unabhängig. Im Gegensatz dazu sind die Durchläufe einer REDUCE() oder SCAN()-Schleife immer vom voherigen Durchlauf abhängig. REDUCE() und SCAN() erfordern als ersten Parameter einen Initialwert, der als Argument für den ersten Aufruf des Callbacks verwendet wird.
REDUCE()erzeugt eine Schleife, die für jedes Element eines Bereichs den Callback ausführt. Diese Funktion erhält als ersten Parameter, das Callback-Ergebnis des vorherigen Durchlaufs und als zweiten Parameter. Das Ergebnis vonREDUCE()ist das Ergebnis des letzten Aufrufs der Schleifenfunktion.SCAN()ist eine Variante vonREDUCE(). WährendREDUCE()nur das letzte Ergebnis der Callbacks ausgibt, erzeugtSCAN()einen Vektor mit allen Ergebnissen der Callback-Aufrufe.
Die Map-Reduce-Funktionen dürfen nur einzelne Werte erzeugen. Datenstrukturen sind auch dann nicht erlaubt, wenn sie alle die gleiche Länge haben und sich in einen rechteckigen Bereich zusammenfügen liessen. Diese Beschränkung gilt auch, wenn die Funktionsergebnisse als Zwischenschritt an eine Kombinationsfunktion für Vektoren (z.B. VSTAPELN()) verknüpft werden. Erzeugt ein Callback eine Datenstruktur, dann erzeugt die jeweilige Funktion den Fehlerwert #KALK!.
Einzig die Funktion REDUCE() darf Datenstrukturen erzeugen; weil diese Funktion nur ein Ergebnis haben kann.
Diese Einschränkung bedeutet, dass die Funktionen NACHSPALTE() und NACHZEILE() die Identitätsfunktion nicht als Callback akzeptieren.
9.8.2 Index-Schleifen mit MATRIXERSTELLEN()
Während die Funktionen der Map-Reduce-Familie Werte voraussetzen, ist dies nicht immer möglich. Die Funktion MATRIXERSTELLEN() erzeugt eine Schleife über zwei Iteratoren, für die Dimensionen der gewünschten Matrix. Der Callback für die Funktion erfordert deshalb 2 Parameter für die beiden Indizes.
Die Funktion MATRIXERSTELLEN() kann meistens durch das äussere Produkt (Kapitel 13) ersetzt werden.
Der Callback für MATRIXERSTELLEN() darf nur zwei Parameter haben, denen die aktuellen Index-Werte zugewiesen werden. Daraus ergibt sich, dass im Funktionskörper nur diese beiden Parameter bereitgestellt werden. Komplexere Anwendungen lassen sich mit Closures erzeugen. Dazu wird eine Funktion mit LAMBDA() erzeugt, die zusätzliche Werte oder Datenstrukturen als Parameter unterstützt. Diese Funktion erzeugt anschliessend den Callback für MATRIXERZEUGEN(). Der Callback ist also ein Closure der erzeugenden Funktion. Dadurch kann der Callback die Werte und Datenstrukturen der erzeugenden Funktion beim Aufruf durch die Funktion MATRIXERZEUGEN() ebenfalls verwenden (s. Beispiel 9.12).
Beispiel 9.12 (Matrix mit Closure erstellen) Im Bereich A1:A4 stehen beliebige Zeichenketten.
=MATRIXERSTELLEN(5;3;
LAMBDA(namen;
LAMBDA(a;b;
ZEILENWAHL(namen;
REST(a+b;
ZEILEN(namen))+1)
)
)(A1:A4)
)9.8.3 Neue Funktionen festlegen
Neben Schleifen können mit LAMBDA() neue Funktionen erzeugt werden. Dazu muss in einem Arbeitsblatt ein Name mit der Funktionsdefinition erzeugt werden. Namen werden über das Menüband Formeln mit dem Kommando Namen definieren erzeugt. Dieses Kommando öffnet einen Dialog, über welchen ein Name definiert werden kann(Abbildung 9.4). In diesem Dialog müssen die beiden Felder Name und Bezieht sich auf ausgefüllt werden.
Der Name ist der Bezeichner der neuen Funktion. Hier dürfen keine Namen vorhandener Funktionen oder benannter Bereiche verwendet werden. Das Feld Bezieht sich auf muss eine LAMBDA-Formel mit der Funktionsdefinition beinhalten. Als Bereich sollte immer Arbeitsmappe ausgewählt sein, weil sonst die Funktion auf ein einziges Arbeitsblatt beschränkt wäre. Zur Dokumentation sollte im Feld Kommentar zusätzlich eine Kurzbeschreibung der Funktion angegeben werden. Leider zeigt Excel diesen Kommentar nicht als Kurzhilfe für den Funktionsnamen an.
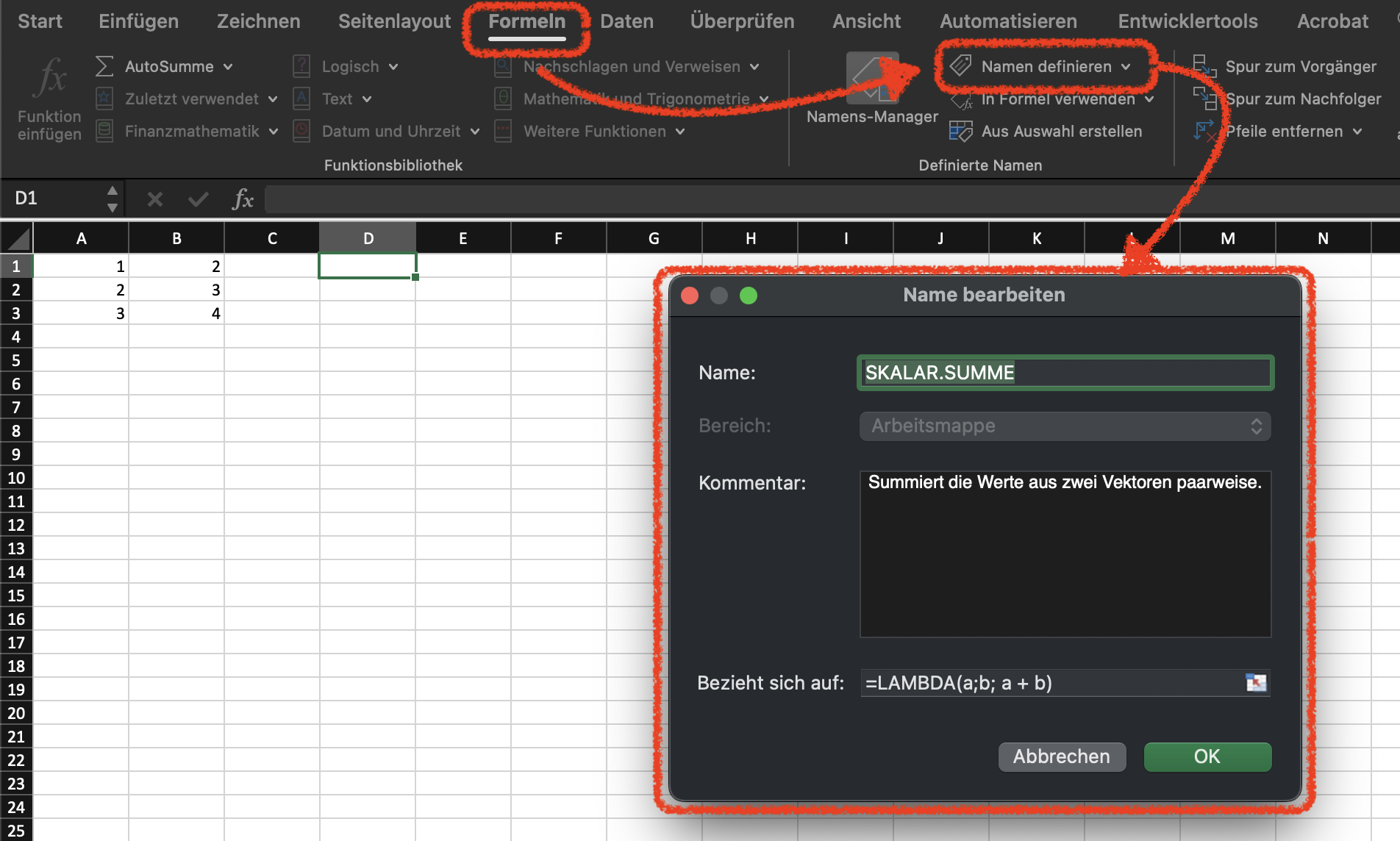
LAMBDA()
Nachdem eine Funktion einem Namen zugewiesen wurde, kann dieser Name wie jede andere Funktion in Formeln verwendet werden (Abbildung 9.5).
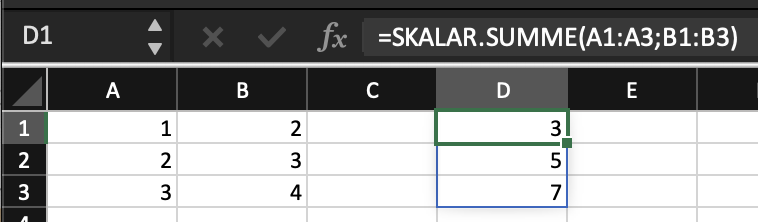
Als Funktionskörper können beliebige Excel Operationen vorkommen. Es bietet sich jedoch an, für komplexere Funktionen den Funktionskörper mit LET() einzuleiten. Dadurch lassen sich einzelne Arbeitsschritte leichter isolieren und verketten.