31.03.2021, von Christian Glahn
Die Normalverteilung ist für die Statistik zentral und viele statistische Methoden setzen voraus, dass die Daten normalverteilt sind. Entsprechend müssen wir immer wieder die Frage beantworten, ob unsere Daten auch hinreichend normalverteilt sind. Diese Frage ist nicht neu und es gibt verschiedene und gut gesicherte Verfahren, um sie zu beantworten. Eine andere nicht so oft gestellte Frage ist, ob unsere Daten überhaupt geeignet sind, um die Normalverteilung statistisch überprüfen zu können. Konkret geht es um die Überprüfung der Normalverteilung, wenn unsere Daten gerundet wurden und unsere Daten sehr homogen sind.
Dazu erinnern wir uns an unsere Statistikeinführung. Dort haben wir sicher gelernt, dass wir nominal-, ordinal- und metrischskalierte Variablen unterscheinden und dass die Normalverteilung nur für metrischskalierte Variablen möglich ist. Damit wir diesen Beitrag nachvollziehen können, erinnern wir uns noch, dass wir die Werte von ordinalskalierten Variablen zwar sortieren können aber die Abstände zwischen den Werten unbekannt sind, weil wir nur bestimmte Werte erhalten. Solche Variablen werden auch als diskret bezeichnet. Als Beispiel kann uns ein Küchenherd dienen: Bei vielen Elektroherden können wir die Hitze der Kochplatten oder -Felder mit einem Regler steuern. Bei meinem Herd gibt es dafür 10 Stufen von 0 bis 9. Ich kann nur die Stufen 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9 auswählen. Ich weiss zwar, dass 8 heisser als 7 und weniger heiss als 9 ist, aber ich kann nicht beurteilen, ob die Temperaturdifferenz auf den Stufen 7, 8 und 9 immer gleich ist. Bei meinem Herd kann ich auch keine halben oder viertel Stufen einstellen.
Im Vergleich dazu ist eine metrischskalierte Variable mit einem Gasherd vergleichbar, bei dem wir stufenlos die Hitze einstellen können. Wenn das Stellrad ein gleichmässiges Gewinde hat, dann entspricht eine halbe Umdrehung des Gashahns immer dem gleichen Zuwachs an durchfliessendem Gas und damit mehr Hitze. Zusätzlich können wir die Umdrehungen nach belieben abstufen, wenn wir etwas weniger Hitze haben wollen. Diese Eigenschaften finden wir auch bei anderen Arten von Daten: Geld ist oft metrischskaliert, Entfernungen sind metrischskaliert und auch die Zeit ist metrischskaliert.
Nun gibt es Daten, die grundsätzlich metrischskaliert sind, wie z.B. die Zeit. In der Praxis reden wir aber je nach Kontext gelegentlich nur über bestimmte Zeitintervalle innerhalb dieses kontinuierlichen Spektrums. In solchen Fällen verwenden wir gerundete Werte. Ein Beispiel für solche gerundeten Werte ist das Alter einer Person. Obwohl das Alter ein kontinuierlicher Zeitraum von der Geburt bis zu einem Zeitpunkt ist, sagt praktisch niemand, dass eine Person 39.5678 Jahre alt sei. Vielmehr runden wir diesen Wert zum letzten ganzen Jahr ab und stellen fest, dass die Person 39 Jahre alt ist.
Wir würden erwarten, dass ein solches Abrunden keinen gewaltigen Effekt auf die Verteilung einer beliebigen Gruppe von Personen hat. Das können wir mit R leicht überprüfen. Dazu erstellen wir uns eine Stichprobe mit normalverteilten Werten um den Mittelwert 30 und einer Standardabweichung von 20.
daten = tibble(o_x = rnorm(101, mean = 30, sd = 20))
Anschliessend runden wir die Werte und behalten sowohl den originalen ungerundeten als auch den gerundeten Wert. Das Ganze visualisieren wir mit ggplot2 als gegenübergestellte Histogramme.
daten %>%
mutate(r_x = floor(o_x)) -> daten_gerundet
daten_gerundet %>%
pivot_longer(everything(), names_to = "nm", values_to = "vl") %>%
ggplot(aes(vl)) +
geom_histogram(aes(y = ..density..), fill = "white", color = "black" ) +
geom_line(stat = "function",
fun = dnorm, args= c(mean = 30, sd = 20), color = "red") +
facet_wrap(vars(nm))
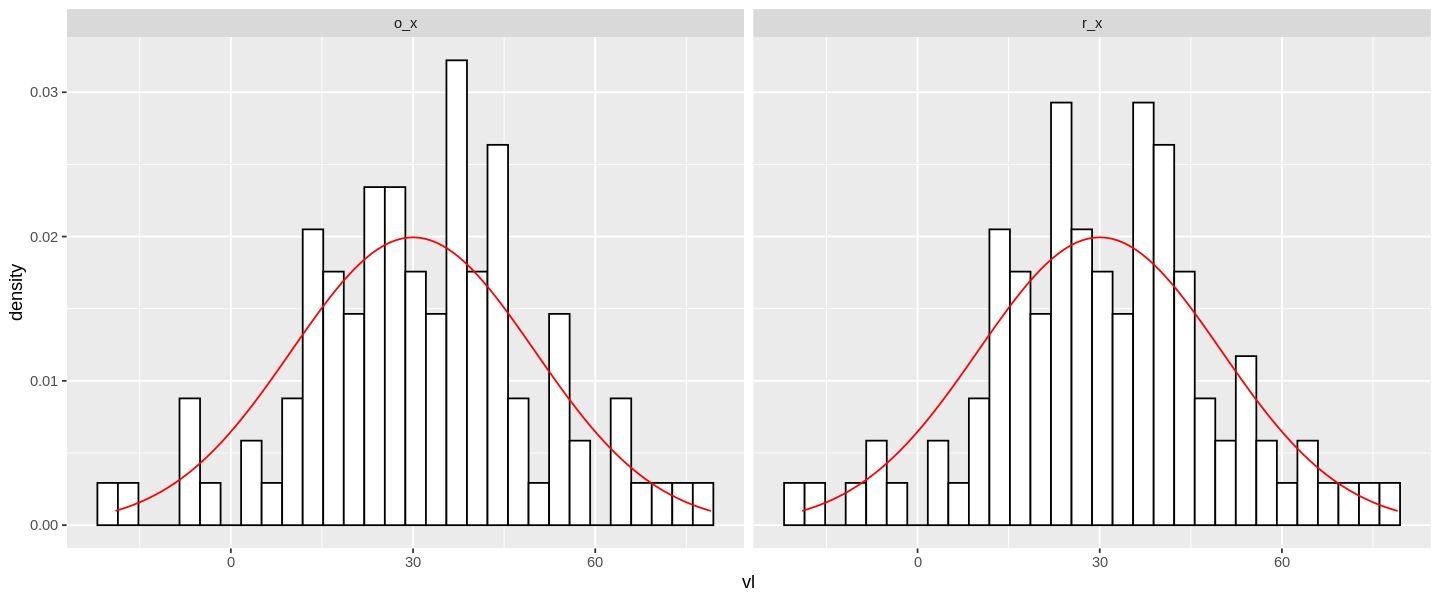
Man erkennt leicht, dass sich die beiden Histogramme für die originalen und gerundeten Werte kaum unterscheiden. Das ist auch nicht weiter verwirrend, da es sich ja die gleichen Werte handelt. Der einzige Unterschied liegt darin, dass das rechte Histogramm die gerundeten Werte berücksichtigt.
Im Histogramm habe ich die Normalverteilung als rote Linie mit eingezeichnet, um die Ähnlichkeit hervorzuheben.
Wir können die Normalität unserer Daten zusätzlich mit anderen Techniken verifizieren. Rein statistisch geht das z.B. mit dem Shapiro-Wilk-Test.
daten_gerundet %>%
summarise(
o_swt = shapiro.test(o_x) %>% tidy() %>% pull("p.value"),
r_swt = shapiro.test(r_x) %>% tidy() %>% pull("p.value")
)
Hinweis: Ich verwende hier die tidy()-Funktion der broom-Bibliothek, damit ich mit dem Ergebnis wie mit einem normalen Daten-Frame weiterarbeiten kann.
| o_swt | r_swt |
|---|---|
| <dbl> | <dbl> |
| 0.7582778 | 0.7423585 |
In beiden Fällen liefert der Shapiro-Wilk-Test eine hohe Wahrscheinlichkeit, dass beide Verteilungen der Normalverteilung ähneln. Das haben wir natürlich auch erwartet. Schauen wir uns zusätzlich noch den Quantile-Plot für unsere Verteilungen an.
daten_gerundet %>%
pivot_longer(everything(), names_to = "nm", values_to = "vl") %>%
ggplot(aes(sample = vl)) +
geom_qq() +
geom_qq_line() +
facet_wrap(vars(nm))
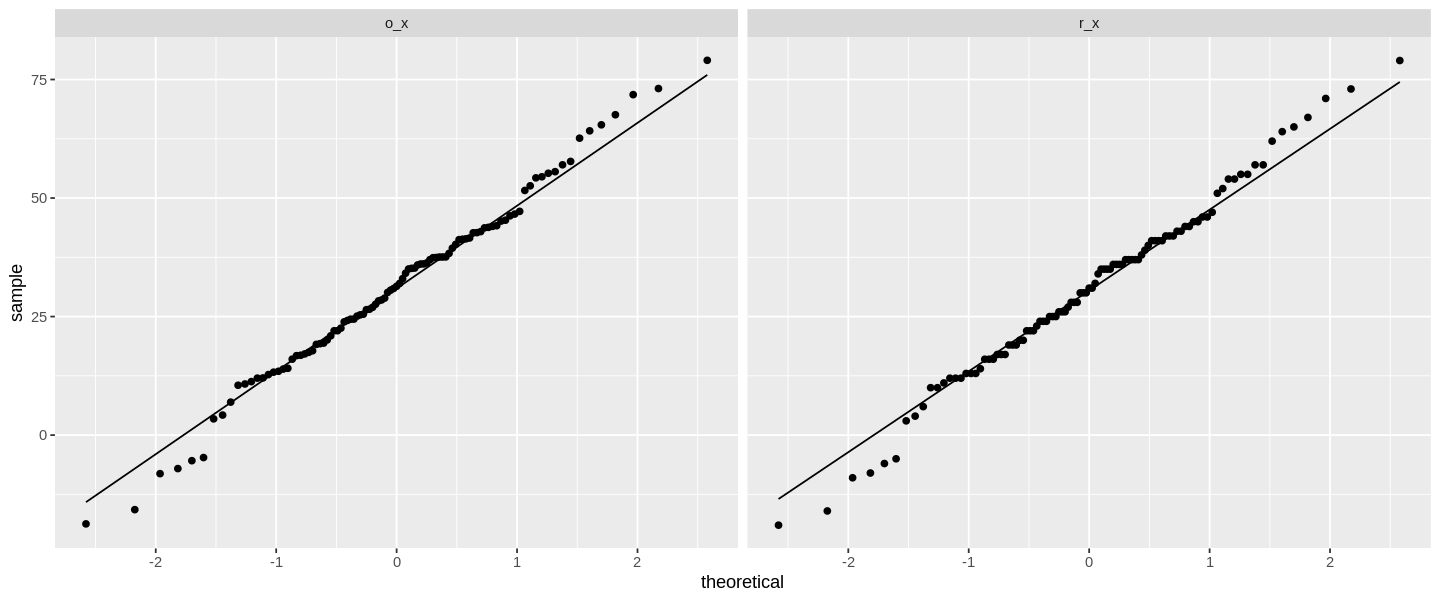
Der Quantile-Plot zeigt schön, dass unsere Werte sehr nah an der theoretisch erwarteten Line der Normalverteilung liegen. Das haben wir natürlich auch so erwartet. Wir sehen sowohl im Shapiro-Wilk-Test und im Quantile-Plot, dass das Runden von Werten einer metrischenskalierten Variable kaum Auswirkungen auf die Einschätzung für eine Normalverteilung hat.
Normalverteilte homogene Stichproben
Leider gibt es im Alltag immer wieder Situationen, in denen diese Aussage nicht ganz zutrifft. Das gilt vor Allem wenn homogene Stichproben vorliegen. Wir erinnern uns wieder an den Statistikunterricht, homogene Stichproben sind Stichproben in denen eines oder mehrere Merkmale nur sehr wenig gestreut sind. Mit anderen Worten, die Standardabweichung (oder die Mittlere Abweichung vom Median) ist klein. Mit klein meine ich Standardabweichungen die kleiner sind als z.B. 5 sind. Das ist kein absoluter Wert, sondern hängt von der Rundung ab: Wenn ich auf eine Nachkommastelle gerundet hätte, dann würde sich klein um Faktor 10 verringern, also z.B. auf 0.5.
Das Veranschaulichen wir uns an der Gruppe der Studienanfänger im 1. Semester. Diese Gruppe ist im Verhältnis zu allen Studierenden im gleichen Studiengang (oder der Hochschule) bezüglich des Alters sehr homogen. Die Standardabweichung liegt dabei in der Regel um 3 Jahre.
Wiederholen wir unser Experiment mit einer ähnlichen Stichprobe.
tibble(o_x = rnorm(101, mean = 25, sd = 3)) %>%
mutate(
r_x = floor(o_x)
) -> daten_homogen
daten_homogen %>%
pivot_longer(everything(), names_to = "namen", values_to = "werte") %>%
ggplot(aes(werte)) +
geom_histogram(aes(y = ..density..), binwidth = 1,
fill = "white", color = "black" ) +
geom_line(stat = "function",
fun = dnorm, args= c(mean = 25, sd = 3), color = "red") +
facet_wrap(vars(namen))
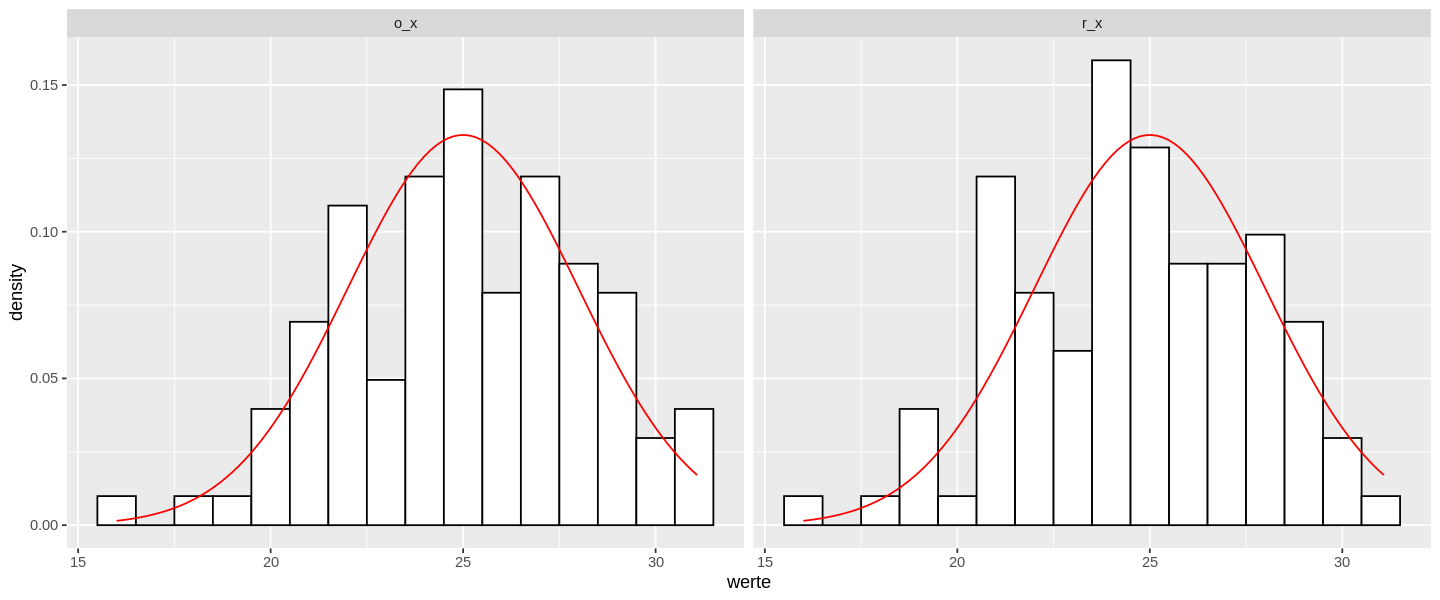
Die beiden Verteilungen sehen eigentlich gut aus und ich würden keine Unterschiede bezüglich der Normalverteilung erwarten. Das prüfe ich mit dem Shapiro-Wilk-Test.
daten_homogen %>%
summarise(
o_swt = shapiro.test(o_x) %>% tidy() %>% pull("p.value"),
r_swt = shapiro.test(r_x) %>% tidy() %>% pull("p.value")
)
| o_swt | r_swt |
|---|---|
| <dbl> | <dbl> |
| 0.4695755 | 0.09376193 |
Hier sehen wir einen deutlichen Unterschied zwischen den beiden Verteilungen. Die gerundeten Werte werden nämlich nicht mehr eindeutig als normalverteilt erkannt, weil der p-Wert für die Verteilung der gerundeten Werte kleiner als 0.1 aber immer noch grösser als 0.05 ist.
Betrachten wir also auch den Quantile-Plot für diese Daten:
daten_homogen %>%
pivot_longer(everything(), names_to = "namen", values_to = "werte") %>%
ggplot(aes(sample = werte)) +
geom_qq() +
geom_qq_line() +
facet_wrap(vars(namen))
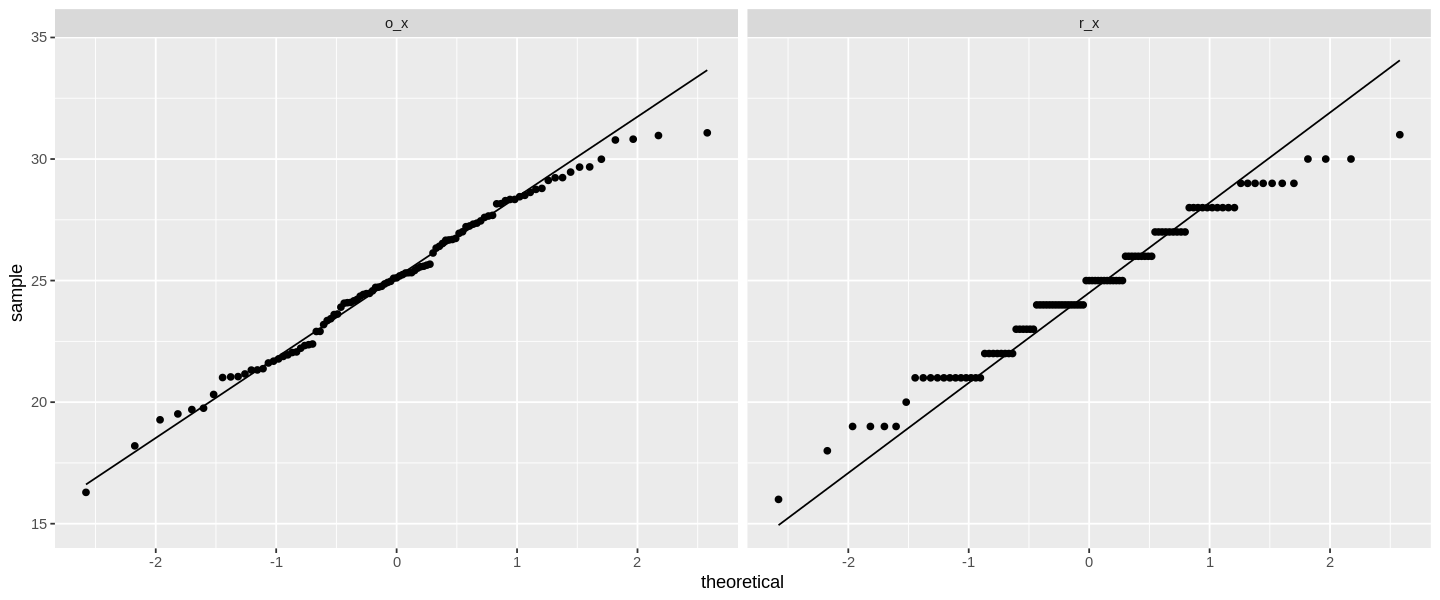
Im Plot sehen wir für die gerundeten Daten zwar noch eine deutliche Nähe zur theoretischen Verteilung, die Daten liegen aber nicht wie die originalen Werte an der Linie, sondern verlaufen irgendwie quer zur theoretischen Vorhersage.
Dieses Bild ist nicht völlig unerwartet, weil die gerundeten Daten nur bestimmte Werte annehmen können. Ein solches Bild ist übrigens typisch, wenn wir ordinalskalierte Daten auf ihre Normalverteilung prüfen.
Dramatisch wird es, wenn eine grössere Stichprobe vorliegt. Für grössere Stichproben würden wir uns normalerweise eine bessere Passung unserer Daten erwarten. Das bedeutet, dass wir eigentlich eine Normalverteilung erkennen müssten.
tibble(o_x = rnorm(301, mean = 25, sd = 3)) %>%
mutate(
r_x = floor(o_x)
) %>%
summarise(
o_swt = shapiro.test(o_x) %>% tidy() %>% pull("p.value") ,
r_swt = shapiro.test(r_x) %>% tidy() %>% pull("p.value")
)
| o_swt | r_swt |
|---|---|
| <dbl> | <dbl> |
| 0.7661587 | 0.01650833 |
Beobachtungen verallgemeinern
Unsere originalen Daten sind weiterhin klar normalverteilt. Das wissen wir, weil ich die Daten für eine Grundgesamtheit mit dem Mittelwert 25 und der Standardabweichung von 3 erzeugt habe. Der Shapiro-Wilk-Test bestätigt das für die ungerundeten Werte. Für die gerundeten Daten müsste ich aber wegen des Shapiro-Wilk-Tests die Normalverteilung ablehnen.
Dieses Ergebnis kann natürlich nur ein einmaliges konstruiertes Ereignis sein. Damit wir die Beobachtung Verallgemeinern können, brauchen wir mehr Beobachtungen. Dazu mache ich ein grösseres Experiment: Ich erzeuge jeweils 100 Zufallsstichproben mit dem Umfang von 100 sowie 300 Werten für die Standardabweichungen zwischen 1 bis 7. Ich verwende die expand-Funktion, um alle Permutationen von 100 und 300 mit den Standardabweichungen von 1-7 zu erhalten. Mit diesen Werten erzeuge ich meine Zufallsstichproben im nächsten Schritt.
Für unser Experiment ist der Mittelwert egal, deshalb nehme ich den Konstanten Wert von 25, um Durchschnittliche FH Studierende zu im 1. oder 2. Semester zu simulieren. Ich erzeuge jede dieser Stichproben wie die Beispielstichprobe oben mit tibble(d = rnorm(n, mean = 25, sd = v), wobei n der Stichprobenumfang und v die Varianz der Stichprobe ist.
Damit ich die Werte paarweise vergleichen kann, runde ich die Ergebnisse wie oben. Abschliessend führe ich den Shapiro-Wilk-Test für die ungerundeten und die gerundeten Werte in jeder der erzeugten Stichproben durch. Weil wir uns nur für den p-Wert interessieren, extrahiere ich diesen Wert mit tidy() %>% pull(). Damit wir leichter weiterarbeiten können, extrahiere ich diese Ergebnisse in die Vektoren swt_orig und swt_rund.
tibble(sz = c(100, 300)) %>%
expand(sz, sd = seq(1, 7)) %>%
mutate(
ds = map2(sz, sd, (function(n, v)
seq(1, 100) %>% map((function(m)
tibble(d = rnorm(n, mean = 25, sd = v)) %>%
mutate(
dr = floor(d)
) %>%
summarise(
swt_orig = shapiro.test(d) %>% tidy() %>% pull("p.value"),
swt_rund = shapiro.test(dr) %>% tidy() %>% pull("p.value")
)
)
)
)
),
ll = lengths(ds),
swt_orig = ds %>% map(function(d) d %>% map(pull,var = "swt_orig")),
swt_rund = ds %>% map(function(d) d %>% map(pull,var = "swt_rund"))
) %>%
select(-c(ds)) -> simds
Jetzt habe ich 2800 Stichproben Shapiro-Wilk-Tests für 1400 Zufallsstichproben durchgeführt. Für jede der Stichproben habe ich den Shapiro-Wilk-Test jeweils für die ungerundeten und die gerundeten Werte der gleichen Stichprobe berechnet. Ich tu also so, als ob ich für die Stichproben jeweils das exakte und das gerundete Alter kenne. Damit stelle ich die Vergleichbarkeit unserer Ergebnisse durchgängig sicher, denn wir wissen, dass für jeden p-Wert für gerundete Werte ein p-Wert für ungerundete Werte gehört.
Mit dieser Vorarbeit können wir für diese Daten Hypothesen formulieren. Meine ersten Beobachtungen lassen zwei mögliche Hypothesen zu.
- Für gerundete Werte bestätigt der Shapiro-Wilk-Test die Normalverteilung seltener als für ungerundete Werte.
- Der Shapiro-Wilk-Test bestätigt die Normalverteilung für gerundete und ungerundete Werte gleich häufig.
Diese Hypothesen kann ich mit den simulierten Ergebnissen überprüfen. Weil ich Zufallsstichproben erstellt habe, werden die Ergebnisse mehr oder weniger normalverteilt um die häufigsten Werte für den Shapiro-Wilk-Test für eine bestimmte Standardabweichung liegen. Also berechne ich den Mittelwert und die Standardabweichung für die einzelnen Stichprobengruppen. Die Funktion map_dbl erledigt den Grossteil des Jobs für uns. Die innere Funktion, die ich an map_dbl übergebe, sorgt dafür, dass die Werte als Vektor an die jeweilige Funktion übergeben werden können.
Neben den Lagemassen bestimme ich noch die Anzahl der Stichproben, die durch den Shapiro-Wilk-Test als hinreichend normalverteilt erkannt wurden. Diese Zahl bestimme ich jeweils für das 95%-Konfidenzintervall sowie wie für das strengere 90% Konfidenzintervall. Weil ich 100 Stichproben erzeugt habe, sind diese Werte gleich den Prozentwerten.
Die Vektoren mit dem Abfang o_ verweisen auf die Ergebnisse der ungerundeten Werte. Die Vektoren mit dem Anfang r_ beziehen sich auf die gerundeten Werte.
simds %>%
mutate(
# ungerundete Werte
o_mw = swt_orig %>% map_dbl(function(x) x %>% unlist %>% mean),
o_sd = swt_orig %>% map_dbl(function(x) x %>% unlist %>% sd),
o_n90 = swt_orig %>% map_dbl(function(x) ifelse(x %>% unlist > 0.1, 1, 0) %>% sum),
o_n95 = swt_orig %>% map_dbl(function(x) ifelse(x %>% unlist > 0.05, 1, 0) %>% sum),
# gerundete Werte
r_mw = swt_rund %>% map_dbl(function(x) x %>% unlist %>% mean),
r_sd = swt_rund %>% map_dbl(function(x) x %>% unlist %>% sd),
r_n90 = swt_rund %>% map_dbl(function(x) ifelse(x %>% unlist > 0.1 , 1, 0) %>% sum),
r_n95 = swt_rund %>% map_dbl(function(x) ifelse(x %>% unlist > 0.05 , 1, 0) %>% sum),
) %>%
select(-starts_with("swt")) %>%
arrange(sd) -> sim_res
sim_res
| sz | sd | ll | o_mw | o_sd | o_n90 | o_n95 | r_mw | r_sd | r_n90 | r_n95 |
|---|---|---|---|---|---|---|---|---|---|---|
| <dbl> | <int> | <int> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 100 | 1 | 100 | 0.5274951 | 0.2891409 | 92 | 96 | 1.050969e-05 | 1.556370e-05 | 0 | 0 |
| 300 | 1 | 100 | 0.5196917 | 0.3037655 | 87 | 94 | 1.981378e-11 | 2.557004e-11 | 0 | 0 |
| 100 | 2 | 100 | 0.4635255 | 0.3024703 | 84 | 89 | 2.281296e-02 | 2.610167e-02 | 2 | 12 |
| 300 | 2 | 100 | 0.4763649 | 0.2686310 | 91 | 96 | 6.607675e-05 | 7.466181e-05 | 0 | 0 |
| 100 | 3 | 100 | 0.5271164 | 0.2724495 | 94 | 96 | 1.355401e-01 | 1.109334e-01 | 49 | 78 |
| 300 | 3 | 100 | 0.4919047 | 0.2997262 | 88 | 94 | 7.669087e-03 | 7.224085e-03 | 0 | 0 |
| 100 | 4 | 100 | 0.4655805 | 0.2983864 | 83 | 91 | 2.325318e-01 | 1.888101e-01 | 67 | 80 |
| 300 | 4 | 100 | 0.4539497 | 0.2837617 | 88 | 91 | 4.472703e-02 | 4.036167e-02 | 10 | 32 |
| 100 | 5 | 100 | 0.5029088 | 0.2887666 | 89 | 97 | 3.272665e-01 | 2.230211e-01 | 81 | 90 |
| 300 | 5 | 100 | 0.4803165 | 0.2763079 | 87 | 93 | 1.191972e-01 | 8.625414e-02 | 56 | 73 |
| 100 | 6 | 100 | 0.4894684 | 0.2832150 | 91 | 94 | 3.703226e-01 | 2.552920e-01 | 85 | 93 |
| 300 | 6 | 100 | 0.5076400 | 0.3055214 | 90 | 94 | 2.170836e-01 | 1.704709e-01 | 65 | 79 |
| 100 | 7 | 100 | 0.4664821 | 0.2994581 | 85 | 92 | 3.736853e-01 | 2.578793e-01 | 79 | 90 |
| 300 | 7 | 100 | 0.5345596 | 0.2943685 | 91 | 95 | 2.915232e-01 | 2.043859e-01 | 79 | 88 |
Die Ergebnisse zeigen deutlich, dass der beobachtete Effekt konsistent bei Variablen auftritt, wenn die Werte gerundet sind und die Standardabweichung “klein” ist. Mit wachsender Standardabweichung werden zunehmend mehr Stichproben als normalverteilt erkannt. Diesen Effekt können wir uns mit zwei Diagrammen visuell veranschaulichen.
Stellen wir zuerst die Mittelwerte der Testergebnisse über die jeweilige Standardabweichung dar.
sim_res %>%
ggplot(aes(sd, o_mw)) +
geom_point() +
geom_point(aes(y = r_mw), color = "red") +
scale_y_continuous(limits = c(0, .6), name = "Mittelwert") +
scale_x_continuous(limits = c(1, 7), n.breaks = 7, name = "Standardabweichung Stichprobe") +
geom_hline(yintercept = .1, linetype = "dashed") +
facet_wrap(vars(sz))
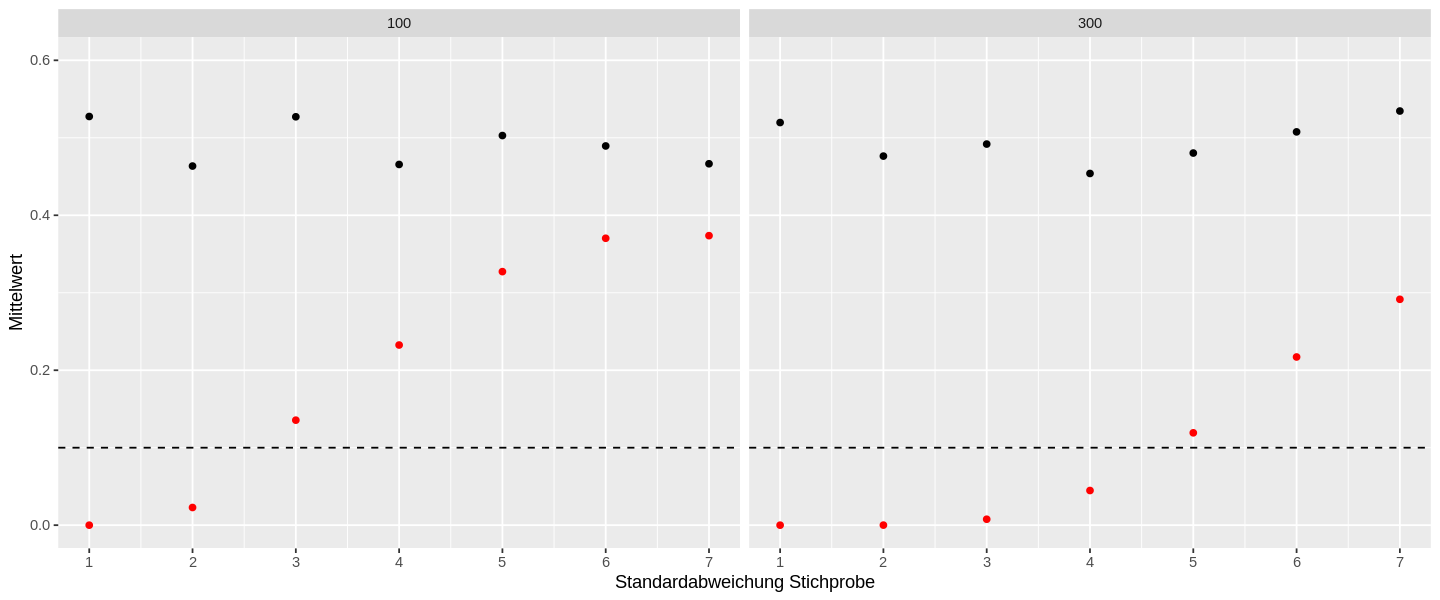
Die schwarzen Punkte zeigen die mittleren Ergebnisse des Shapiro-Wilk-Tests der ungerundeten Werte und die roten Punkte für die gerundeten Werte an. Die horizontale gestrichelte Linie zeigt das Signifikanzniveau ab dem wir eine Normalverteilung akzeptieren würden. Ich habe zusätzlich die beiden Stichprobenumfänge separat dargestellt, damit die Unterschiede mit wachsenden Stichprobenumfang erkennbar werden.
Diese Abbildung zeigt deutlich, dass die Ergebnisse mit grösser werdender Standardabweichung insgesamt zutreffende Ergebnisse liefern. Diese Gegenüberstellung zeigt uns allerdings nicht, wie viele dieser normalverteilten Stichproben wir als hinreichend normalverteilt akzeptiert hätten. Zu diesem Zweck erstelle ich ein zweites Diagramm, das die Anzahl der als hinreichend normalverteilt erkannten Stichproben im 5% Signifikanzniveau gegenüberstellt.
sim_res %>%
ungroup() %>%
ggplot(aes(sd, o_n95)) +
geom_point() +
geom_point(aes(y = r_n95), color = "red") +
scale_y_continuous(limits = c(0, 100), name = "Erkannte Stichproben") +
scale_x_continuous(limits = c(1, 7), n.breaks = 7, name = "Standardabweichung Stichprobe") +
facet_wrap(vars(sz))
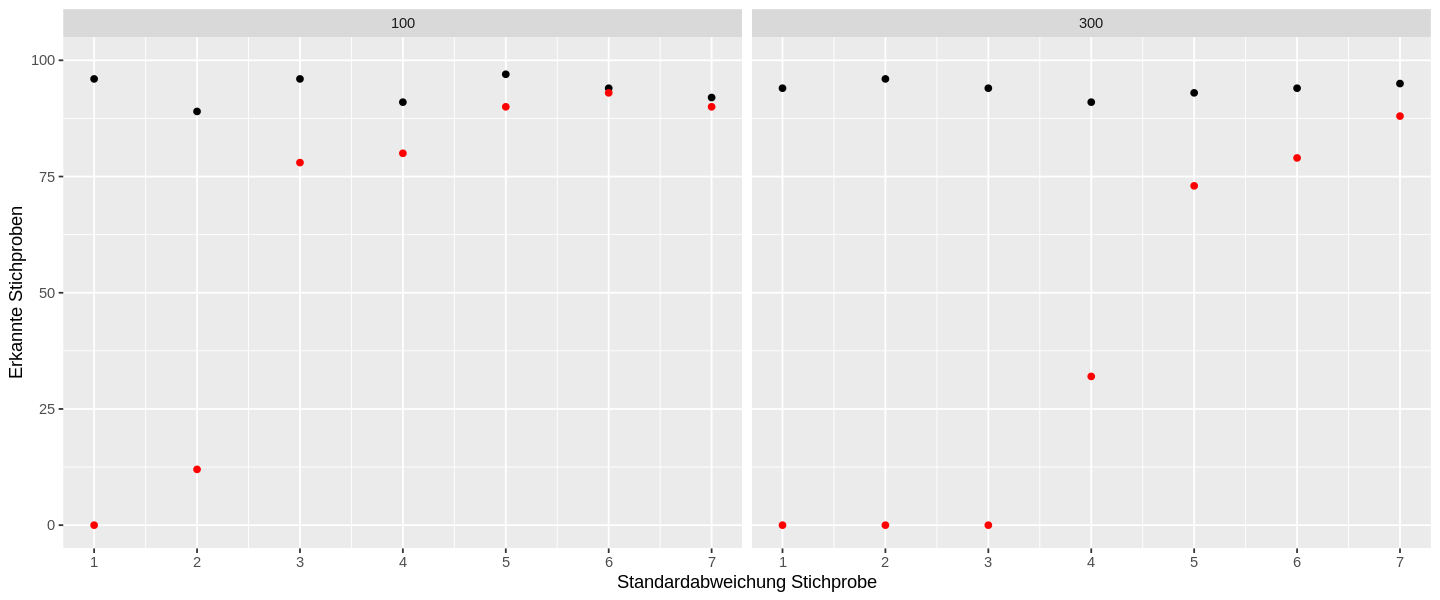
Diese Darstellung zeigt schön, dass wir nicht die perfekte Normalverteilung erkennen müssen, um eine Stichprobe noch als hinreichend normalverteilt zu erkennen. Vielmehr werden bei ungerundeten Werten fast alle Stichproben als hinreichend normalverteilt erkannt. Das Diagramm zeigt damit sehr schön, dass wir keine besonders grossen p-Wert erhalten müssen, um eine Stichprobe richtig zuzuordnen.
Für die in Rot dargestellten gerundeten Werte erkennen wir, dass bei kleinen Standardabweichungen die Trefferquote sehr gering ist. Eine gute Trefferquote liegt im Bereich oberhalb ab 90% (bzw. 90 korrekt als normalverteilt erkannten Stichproben). Damit verwerfen wir nur 10% der Stichproben, die aus eigentlich normalverteilten Grundgesamtheiten stammen. Dieser Wert entspricht dem empfohlenen Signifikanzniveaus von 10% für diesen Test. Das 5%-Signifikanzniveau für diesen Test wird auch für Zufallsstichproben mit ungerundeten Werte kaum erreicht.
Diese Abbildung veranschaulicht auch gut, dass der Shapiro-Wilk-Test für grössere Stichproben weniger zuverlässige Ergebnisse liefert: Bei Stichprobenumfängen von 100 werden bereits ab einer Standardabweichung von 4 fast die geleiche Anzahl von Stichproben mit gerundeten Werten erkannt, wie bei den ungerundeten. Bei einem Stichprobenumfang von 300, erhalten wir erst ab einer Standardabweichung von 6 ähnlich gute Treffgenauigkeiten für die gerundeten Werte wie für die ungerundeten.
Fazit
Die Ergebnisse erlauben uns, die beiden Hypothesen gegenüberstellen. Die Ergebnisse der Simulation zeigen deutlich, dass der Shapiro-Wilk-Test die Normalverteilung seltener bestätigt als für ungerundete Werte (Hypothese 1), wenn die Standardabweichung klein ist. Wenn die Standardabweichung grösser wird, dann trifft die 2. Hypothese zu: Der Shapiro-Wilk-Test bestätigt die Normalverteilung für gerundete und ungerundete Werte gleich häufig. Die Gültigkeit der beiden Hypothesen geht ineinander über, je grösser die Standardabweichung wird. Unser Experiment hat gezeigt, dass der Stichprobenumfang die Grenze beeinflusst, ab der die Normalverteilung für gerundete und ungerundete Werte gleich gut identifiziert wird.
Wenn uns metrisch skalierte Variablen mit gerundeten Werten vorliegen, dann müssen wir aufpassen, besonders wenn die Stichprobe sehr homogen verteilt bzw. die Standardabweichung der Stichprobe klein ist. In der oben gezeigten Simulation ist uns die Grundgesamtheit bekannt und wir wissen, dass jede der 1400 Stichproben eigentlich normalverteilt ist. Trotzdem haben wir zufällige Schwankungen in den simulierten Verteilungen. Diese Schwankungen können so gross sein, dass eine Verteilung nicht mehr korrekt mit Hilfe des Shapiro-Wilk-Tests einer normalverteilen Grundgesamtheit zugeordnet werden kann. Liegen die Werte auch noch gerundet vor und sind sie nicht breit genug gestreut, dann erscheinen die Daten aus Sicht des Tests als diskret. Weil für die Normalverteilung, nominal- und ordinalskalierte Skalenniveaus nicht zulässig sind, lehnt der Shapiro-Wilk-Test sehr homogene Verteilungen tendenziell als nicht normalverteilt ab.
Ab wann kann man bei gerundeten Werten von einer kleinen Standardabweichung sprechen?
Abschliessend gehe ich noch auf diese Frage ein, denn wie ich schon Eingangs festgestellt habe, ist eine kleine Standardabweichung relativ. Grundsätzlich gilt hier, dass eine kleine Standardabweichung dann vorliegt, wenn sie in der gleichen Grössenordnung wie die Rundung liegt. In diesem Fall können wir Zwischenschritte zwischen den gerundeten Werten nicht mehr differenzieren und aus der Perspektive des Shapiro-Wilk-Tests erscheinen die Daten als diskret skaliert. Runden wir auf ganze Zahlen, dann liegen kleine Standardabweichungen oft zwischen 1 und 10. Runden wir auf eine Dezimalstelle, dann liegen kleine Standardabweichungen zwischen 0.1 und 1.
Dieser Blog-Beitrag wurde mit Jupyter Lab erstellt. Alle Grafiken wurden mit ggplot2 aus den Daten erzeugt.